I co-wrote an introductory paper on Bloom filters that highlights some iterative and revolutionary improvements, like the Cuckoo filter, along with the everyday and novel uses of the algorithm. The paper was published on the arXiv. Read on to learn more about Bloom filters and my paper!
Zach, a friend and teammate of mine, and I decided we were particularly interested in Bloom filters, and, having experience writing research papers, decided to write a survey paper on Bloom filters, including their modern improvements and applications. Inspired by Dr. Pettie’s creative titles, Zach and I wrote In oder Aus1.
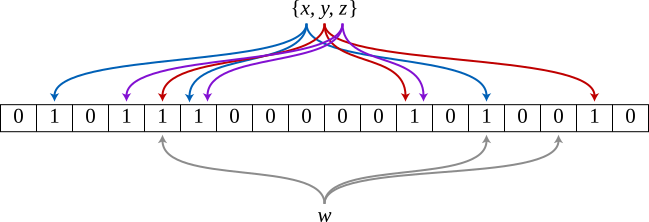
An example Bloom filter storing the set $\lbrace x,y,z\rbrace$ with hash functions. Each of $x$, $y$, and $z$ is mapped by three unique hash functions to three bits. $w$ is queried by checking the three bits that it hashes to. Since one of $w$’s corresponding bits is unset, the query will return false.
As described in the paper, Bloom filters are data structures used to determine set membership of elements in true constant time with reduced memory consumption. A trivial real-world example of Bloom filters in action is browsers checking for malicious URLs; rather than ship a list of millions of URLs to check a URL against (in linear time), browser vendors include a Bloom filter on the order of several megabytes in which the target URL is queried for quickly. If the Bloom filter returns “false”, the site is safe! (Basically, Bloom filters are the most efficient way to check if something is in a set.)
In the paper, we discuss more interesting variations of the Bloom filter, which add features such as element deletion and/or reduce space cost or cache misses; as well as groundbreaking practical applications such as de novo genome assembly, where the use of Bloom filters has dramatically decreased the cost.
Below is a table from the paper comparing the characteristics of Bloom filters, their extensions, and variations. The cache misses column corresponds to real-world performance, and shows the worst-case. In the General Bloom and the Blocked Bloom designs, $h$ indicates the number of hash functions used. In the $d$-Left Counting Bloom construction, $d$ is the number of partitions in its hash table. As explained in the following section, $f$ is the number of completed fuzzy-folds.
| Filter type | Relative space cost | Cache misses per lookup | Deletion support |
|---|---|---|---|
| General Bloom | 1 | $h$ | No |
| Counting Bloom | $3\sim 4$ | $h$ | Yes |
| Blocked Bloom | $1$ | 1 | No |
| $d$-Left Counting Bloom | $1.5\sim 2$ | $d$ | Yes |
| Quotient | $1\sim 1.2$ | $\geq 1$ | Yes |
| Fuzzy-Folded Bloom | $\sim 0.5$ | $h(f+2)$ | No |
| Cuckoo | $\leq 1$ | 2 | Yes |
Abstract
Bloom filters are data structures used to determine set membership of elements, with applications from string matching to networking and security problems. These structures are favored because of their reduced memory consumption and fast wallclock and asymptotic time bounds. Generally, Bloom filters maintain constant membership query time, making them very fast in their niche. However, they are limited in their lack of a removal operation, as well as by their probabilistic nature. In this paper, we discuss various iterations of and alternatives to the generic Bloom filter that have been researched and implemented to overcome their inherent limitations. Bloom filters, especially when used in conjunction with other data structures, are still powerful and efficient data structures; we further discuss their use in industry and research to optimize resource utilization.
This is, of course, a psuedo-German gibberish resembling a translation of “in or out” (as in, an element’s set membership), and a nod to a legendary comedian.] ↩︎